L'estudi acurat de la balística de les fletxes en l'atmòsfera és d'una complexitat extraordinària, i gaire bé inabastable si es vol descendir molt en el detall de tots els efectes a considerar. La forma més corrent d'afrontar el problema és amb el model de massa puntual, tal com acostuma a fer-se en la balística de les armes curtes de foc. En projectils d'artilleria pesada i per míssils cal considerar tot un seguit d'efectes més si es vol una certa precisió.

En el rang de velocitats abastable per les fletxes es pot considerar que la força de fregament amb l'aire es proporcional al quadrat de la velocitat :

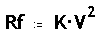
De tal manera que l'acceleració de frenat que experimenta una fletxa pel fregament amb l'aire, és en les seves components :

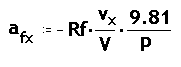
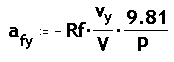
on K és una constant que depen de la forma de la fletxa i de les seves plumes, i que segons el model de W.J. Rheingans és :

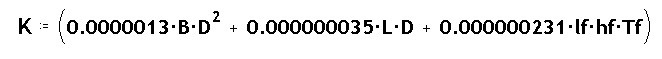
on B és un coeficient pel tipus de punta emprat, que per puntes parabòliques és de 1; D és el diàmetre de la tija de la fletxa, L n'és la longitud, Tf és un coeficient que indica el tipus de pluma emprada, que per plumes de plàstic val 1, i per plumes naturals 2, lf és la longitud de la pluma, i hf n'és l'alçada. Totes les mides en polzades.

En el sistema mètric, i donant totes les mides en mm, excepte la longitud de la fletxa en cm, K és :

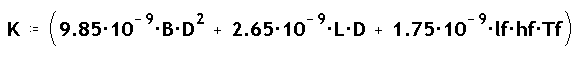
K és doncs la suma de tres factors, en la que el primer dóna la resistència deguda a la punta i a la secció de la fletxa, el segon dóna la resistència provocada per la superfície de la fletxa, i el tercer la provocada per la superfície de les plumes.

Les equacions que cal resoldre per determinar la trajectòria d'un projectil en aquest model són :

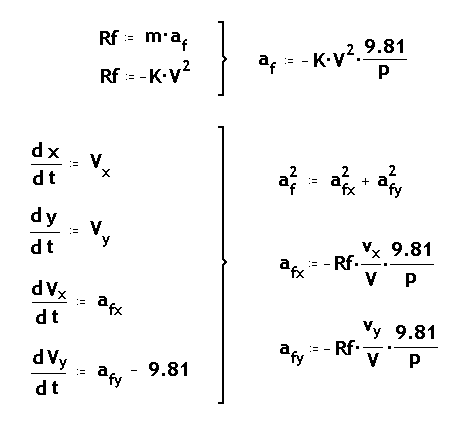
Sistema d'equacions diferencials acoblades que només resoldrem numèricament, al prendre passos prou petits com perquè es pugui considerar que la força de fregament amb l'aire és constant en aquest tram. El mètode numèric emprat de forma més corrent és el Runge-Kutta de quart ordre, que demana el càlcul de quatre punts per intèrval per a cadescuna de les variables : X, Y, Vx, i Vy en un cas de dues dimensions. Es donen tot seguit les equacions per al càlcul de Y_i+1 :

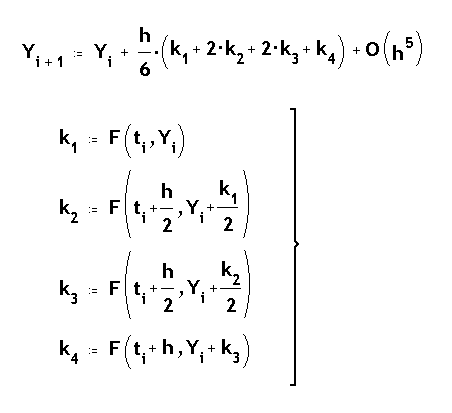
on h és l'intèrval constant de temps considerat, i F(t_i,Y_i) representa la derivada de Y respecte a t en el punt i. Es farà el mateix per a les altres variables, i per a cada intèrval h de la trajectòria. Es prendran no menys de 100 punts per segon per a obtenir un resultat prou bo.

Carregueu el llistat del programa complert en cpp que executa aquests càlculs per veure millor la implementació de tots els detalls.

Anterior

Retorn a Articles