Es coneix per balística interna l'estudi dels mecanismes i les lleis que regeixen sobre la transmissió d'energia a un projectil mentre aquest encara no ha abandonat l'arma que el llença. Vegeu per exemple : "L'arc de politges : Emmagatzemament i restitució d'energia". S'anomena com a balística externa l'estudi de tot allò que passa un cop el projectil ha abandonat l'arma que l'ha llançat i fins a l'impacte. La balística terminal s'ocupa d'estudiar els impactes dels projectils i els seus efectes sobre diferents materials.

Aquí ens ocuparem de la balística externa en el buit. En absència d'atmósfera no hi ha fregament del projectil amb el medi, i l'única força que actua sobre la fletxa un cop ha deixat l'arc és la de la gravetat. La veritat és que el tir amb arc en el buit seria extraordinàriament complicat, i més complexe encara que tirar les fletxes sense plumes. Tant mateix és útil la idealització d'un model basat en un projectil de massa puntual per la informació que ens aportarà. La trajectòria d'un cos llançat en el buit correspon a una paràbola simètrica que en un cas general podem representar com :

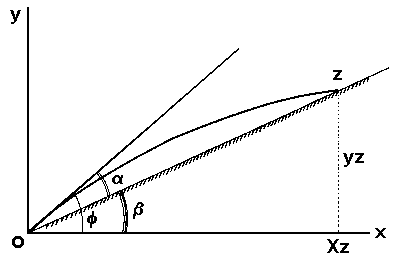
Fig 1 : Trajectòria ideal

On b dóna el pendent del terreny, a és l'angle d'elevació del tir respecte la línia de visió, i f és l'angle d'elevació del tir respecte la horitzontal. Es té que f = a + b.

En aquestes condicions la distància OZ que recorrerá la fletxa abans d'impactar amb el terra, amb Xz l'abcisa que li correspon, venen donadades per :

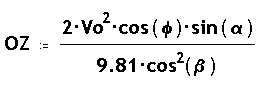
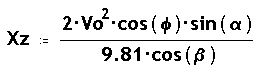
La simplicitat del model en el buit permet representar tota la trajectòria de la fletxa, des que deixa l'arc, en un simple full de càlcul, on en cada fila de la taula es representin el valor de les variables rellevants en un punt d'aquesta trajectòria. Partint d'uns valors inicials de coordenades Xo i Yo, i de velocitat Vo, es calcularan els valors successius de la trajectòria a uns increments fixes d'abcissa Dx, com :
 

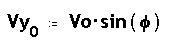
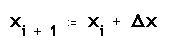
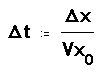
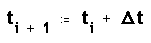
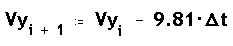
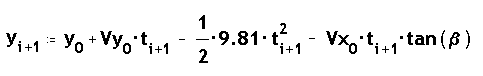
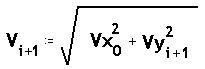
On Vxo i Vyo són les components de la velocitat inicial, t és el temps transcorregut des de l'inici, X són les abcisses, i Y les ordenades corregides respecte la línia del terra, de manera que Yz sigui 0.

Finalment la inclinació de la fletxa en cada punt de la trajectòria ens ve donada per l'angle :

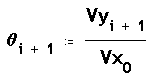
Podem recollir-ho tot en un full de càlcul com el següent :

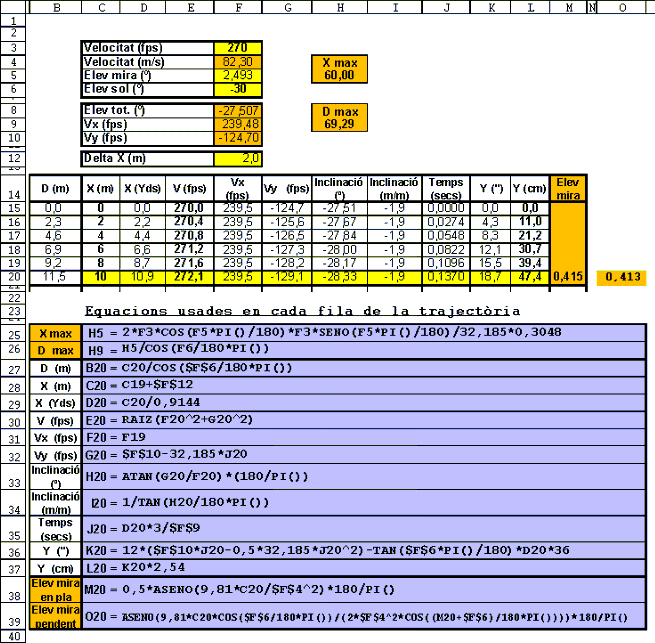
On s'il·lustra la trajectòria fins a 10 metres en increments de 2, en les files 15 a 20. Aquesta trajectòria pot extendre's el que calgui afegint-hi les files necessàries. Al cap de vall es donen les equacions tal com han estat emprades en cada casella del full de càlcul. [Alerta als canvis d'unitats i als factors corresponents].

Per altra banda l'elevació de tir que cal per llançar un projectil en el buit a una diana en pla que es troba a una distància Xz ve donada per :

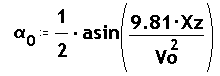
mentre que si el tir és sobre una diana elevada un angle b, l'elevació de mira per impactar-la vindrà donada per :

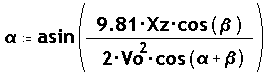
que s'haurà de resoldre iterativament en dependre del mateix valor de a. La solució inicial que es prendrà és el valor de l'elevació a que correspon a una distància D·cos(b), és a dir la distància horitzontal que ens separa de la diana.

Podeu carregar un fitxer Excel amb un full de càlcul per un projectil a 270 fps, un altre a 140 fps, i un altre a 1000 fps, com a exemples. Les velocitats s'hi poden canviar directament. El fitxer Excel també conté un full pel càlcul de les mides de visor per tir en pla, i un altre per les pendents on es pot veure com afrontar els tirs cara amunt o cara avall, i que ofereix la possibilitat d'experimentar amb diferentes velocitats i diferents angles d'inclinació.

En el següent capítol hi ha indicacions sobre el funcionament d'aquest full de càlcul.

Retorn a Articles

Següent